My company is doing open enrollment again for next year (for more info on what to choose in open enrollment, see previous posts). I’m not going to make any changes except I have to re-enroll for flexible spending account (FSA).
If you use flexible spending account, you should be familiar with the use-it-or-lose-it rule. If you put too much in the FSA, you will lose what you can’t use. In the past I always estimated conservatively. I’ve never lost any money to the FSA. However there is also a cost to that approach. After the money in the FSA is used up, any additional expenses must be paid with after-tax dollars. There has to be a point where losing a little pre-tax money in the FSA is less expensive than paying a lot with after-tax money.
This becomes an interesting math problem.
Suppose your best estimate for next year’s FSA-eligible expenses is $1,000, plus or minus $500 because you can never be sure what your actual expenses will be. Your marginal tax rate for FSA contributions is 32% (you have to include the Social Security and Medicare taxes if your income is below the Social Security Wage Base, $106,800 in 2009). How much should be put in your FSA?
So your expenses will range from $500 to $1,500 next year. We can divide it up into ten smaller intervals: $500-600, $600-700, …, $1,400-1,500. For each interval, we use the mid-point as the proxy and calculate the total after-tax cost. The total after-tax cost is:
FSA Contributions * (1 – Marginal Tax Rate) + Expenses Above & Beyond FSA
For example, if you contribute $1,000 to FSA, and your actual eligible expenses are:
| From | To | Midpoint | Total After-Tax Cost |
| 500 | 600 | 550 | 680 |
| 600 | 700 | 650 | 680 |
| 700 | 800 | 750 | 680 |
| 800 | 900 | 850 | 680 |
| 900 | 1,000 | 950 | 680 |
| 1,000 | 1,100 | 1,050 | 730 |
| 1,100 | 1,200 | 1,150 | 830 |
| 1,200 | 1,300 | 1,250 | 930 |
| 1,300 | 1,400 | 1,350 | 1,030 |
| 1,400 | 1,500 | 1,450 | 1,130 |
| Average | 805 |
Over the full range of likely expenses, your average total after-tax cost is $805 if you contribute $1,000 to your FSA. After calculating the same for other contribution amounts, we get this nice graph.
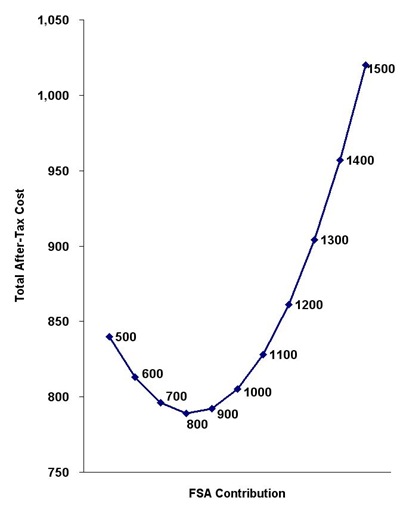
The graph shows that putting in the most conservative amount ($500) isn’t the best strategy. Putting in your best estimate ($1,000) isn’t the best either. The lowest average total after-tax cost over the full range of the estimated expenses is achieved when you put in somewhere in between those two numbers, around $800 in our example.
If you’d like to play with your own numbers, here’s the spreadsheet I created.
Spreadsheet: How Much Should You Put Into Flexible Spending Account (FSA)
Math-minded readers probably noticed that by taking a straight average of the total after-tax costs for all ten intervals, I’m giving each interval equal weight. In math terms, it’s called a uniform distribution. In real life, the intervals at either end of the range ($500-600 and $1,400-1,500) will be less likely than the intervals in the middle. So here’s the challenge question for interested readers:
If you assume your next year’s FSA-eligible expenses follow a normal distribution with a mean of $1,000 and a standard deviation of $250 (same $500 to $1,500 range with 95% confidence), how much should you put into the flexible spending account in order to minimize your expected total after-tax cost?
Who knew a flexible spending account involves this much math?
Finally, if you are married and one of you earns an income above the Social Security Wage Base and another earns below, you should have the spouse with the lower income contribute to the FSA. This was explained by indexfundfan.
Say No To Management Fees
If you are paying an advisor a percentage of your assets, you are paying 5-10x too much. Learn how to find an independent advisor, pay for advice, and only the advice.
Don says
Comment one: I’m a mathematician, and what I usually do is compute my known predictable expenses. I usually add for a pair of glasses, and save that amount. Most years, I’ve used up my account within the last few weeks of the year and I just haven’t bothered to get new glasses. Next year I’m budgeting for new glasses for my wife and for me. It isn’t mathematical, but it works pretty well.
Comment two: I suspect that the normal distribution is probably not correct for this purpose. I suspect a long-tailed distribution is probably more appropriate, like an exponential distribution, because medical expenses aren’t symmetric. Most years you have expenses right around your predicted amount, but on rare occasions you have a lot of expenses (although generally that is capped by out of pocket limits). Just something to think about.
Harry Sit says
Don – Thank you for your comments. I have a column in my spreadsheet for user-specified probabilities. You can assign whatever distribution to the bands.
Debbie M says
Choosing an amount is fascinating. So far I’ve been healthy, so my expected value is pretty close to my minimum value (with a long tail). Except one year my minimum value was actually too high an estimate because my prescription was switched to a generic brand and I found a much cheaper way to get glasses (online).
I hear people with several kids can generally count on at least one expensive thing happening, though.
Fortunately, my company has the three-month post-year grace period thing (which I believe is allowed but not required by law), so I can safely overestimate a little. And with all the little deductibles at the beginning of the year, I can definitely spend more then than in the average month. So far I haven’t had to use it, though.
There are plenty of other fascinating questions such as: Do you include non-urgent things like wisdom tooth removal, hoping that it will force you to finally get around to doing it, or do you keep that out of the equation, fearing that you can’t trust yourself? Do you pay an extra $9 for a debit card, knowing that it will help you actually make your claims, or do you risk not having the card, hoping you’ll actually fax in the forms? I can barely even predict my actions, let alone change in my health, the cost of things, or in the availability of things.
Z says
Is there a maximum contribution amount per employee, per employer, even in instances where the employee terminates and is rehired after 30 days? When an employee is rehired after 30 days at my company, they are treated as a new hire, which means they can re-elect FSA. But is their contribution amount limited to difference of the maximum and what they originally elected?
Ex: I elect $2650 (maximum) and terminate. I am rehired later on in the year with same employer. Can I re-enroll in FSA or am I maxed out? I couldn’t find any IRS regs that point to this.