When the stock market moves up or down, it can knock your asset allocation off your target. Rebalancing means selling the winners and buying the losers in order to bring a portfolio back to its target allocation.
When it comes to rebalancing a portfolio, the 5%-band method is a popular one. It says that you rebalance when the percentage of stocks is at least 5% off your target. For example suppose your target allocation for stocks is 60%, using the 5%-band threshold, you will rebalance when stocks become more than 65% or less than 55% of your portfolio.
What does it take to knock your portfolio’s asset allocation off by 5%? You may be surprised that it takes more than you think. It was a surprise to me as well.
Today’s post is inspired by a post in the Bogleheads investment forum by JimInIllinois. Jim wrote:
“The higher your stock allocation the more stocks have to drop to hit your 5% band. If your target is 90/10 and we assume bonds don’t change then to hit 85/15 your stocks would have to drop by 37%. To go from 75/25 to 70/30 the required drop is 22%, which is a pretty big correction. What really surprised me is that to go from 50/50 to 45/55 still requires stocks to drop 18%.”
I’m interested in the math to calculate the required drop for any given asset allocation.
Suppose I have $1 in my portfolio. $S is invested in stocks and $(1-S) is invested in bonds. Suppose after stocks drop by x and bonds are unchanged, my allocation to stocks is reduced by 5 percentage points. We have:
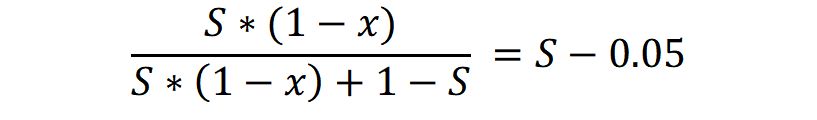
There are only two variables S and x in this equation. We can solve x as a function of S. If you do the algebra, you will get:
x = 0.05 / S / (1.05 – S)
So if S is 90%, x = 0.05 / 0.9 / (1.05 – 0.9) = 0.37. Jim is exactly right: it takes a 37% drop in stock prices to move a portfolio from 90% in stocks to 85% in stocks. If S is 60%, x = 0.05 / 0.60 / (1.05 – 0.6) = 0.19. It takes a 19% drop in stock prices to move a portfolio from 60% in stocks to 55% in stocks.
Putting the numbers in a chart, we have:

Between the “normal” range of 30-80% allocation to stocks, it takes a drop of 18% to 25% to move the needle by 5 percentage points.
We can do a similar calculation for stocks going up and thus increasing the stocks percentage by 5 points. I will skip the math details. The formula comes out to:
x = 0.05 / S / (0.95 – S)
The chart looks like this:

For the stocks-up cases, the bottom line numbers are similar to those for the stocks-down cases, but several points higher. For example it takes a 24% rise in stock prices (as opposed to a 19% drop) to move a portfolio from 60% in stocks to 65% in stocks. If you have 80% in stocks, stocks must gain 42% (as opposed to dropping 25%) before they bump your allocation in stocks to 85%.
Stocks don’t move up or down 20% or 25% every year. This means the 5%-band rebalancing method is quite slow. If you use this method, except in big up or down years, it will probably take several years to trigger a rebalance.
By implication, if you rebalance every year, the change to the allocation percentages must be very small in most years. Say you start with a 60% weight in stocks, by the end of year, it might become 61.3%. The risk and expected returns of a portfolio 60% invested in stocks and a portfolio 61.3% in stocks are practically the same. It’s hardly worth doing anything. You might as well wait until it drifts past 65% or 55%.
Being slow isn’t a bad thing. The markets are said to display short-term momentum. It means when it’s going up, it’s going up for a while and when it’s going down, it’s going down for a while before it changes direction. By waiting longer to rebalance, you let the winners run longer when the market is going up and you wait until prices go lower before you buy.
However, waiting longer also means you won’t be able to catch the 15% dip if you are waiting for a 20% drop for the 5% band to be triggered. There is no way to tell whether a drop is going to reach 20% or just stop and reverse course at 15%.
Because the market goes up more often than down, perhaps asymmetric bands are in order, say 7% up, 3% down?
Note: So far the calculations assumed that bonds are unchanged. We can introduce another variable and make bonds go up or down by b%. Deriving the formula with this extra variable is left as an exercise for the reader.
If you assume negative correlation — stocks down, bonds up, and vice versa — which isn’t the always case as they often have low, but positive correlations, the required drop and increase will be a few points lower than the charts show. If stocks and bonds are both down or both up, the required drop and increase will be a few points higher.
Learn the Nuts and Bolts
I put everything I use to manage my money in a book. My Financial Toolbox guides you to a clear course of action.

thad says
solid – interesting to see the math. being young, I don’t usually pay too much attention to the ebb and flow of the stock market, but I did notice the other day when everything was way down, that my percentages weren’t too far off target (1 or 2%). now I can see why that is.
JimInIllinois says
Thanks for doing the nice charts to get the word out on this.
Since I’m bad at solving equations in my head I used calculus to find a simpler formula for estimating how much daily fluctuations would affect my asset allocation. The sensitivity of the stock or bond percentage to changes in stock prices minus changes in bond prices is the fraction in stocks times the fraction in bonds.
For a 70/30 portfolio the sensitivity is 0.7*0.3=0.21. If stock prices rise 5% and bond prices drop 1% the asset allocation changes by 0.21*(5%-(-1%))=0.21*6%=1.26%. By this formula, the price change needed to hit a 5% rebalancing band at 70/30 is 5%/0.21=24%, which is between the numbers on your rise and fall charts.
For the two decades you’ll spend between 60/40 and 40/60 the sensitivity is between 0.24 and 0.25, so just divide whatever the market did by 4 to find out how much your asset allocation shifted and remember that it takes a 20% change to hit a 5% band.
nickel says
There’s another interesting thread on the Bogleheads forum about how damaging it was to rebalance during Japan’s decline. As I noted in my comment to your previous post yesterday, frequent rebalancing in a falling stock market can amplify your losses, as you continually exchange into a losing investment. Don’t get me wrong – I’m generally on board with this sort of thing, but it’s downright scary to see the numbers out of Japan.
ajk says
I like decimals.
x = .05 / [S (1.05 – S)]
example: S = .90, 1.05 – S = .15, .90 (1.05 – .90) = 0.135
x = .05/.135 = 0.37
I know why .05 is there (you want a 5% change), but I don’t know why your formula has a 50000 in it. [Actually, I do, but why do you want to change a simple 0.05 that is directly understandable by a factor of 1,000,000?]
Harry Sit says
@ajk – I used whole numbers because it makes it easier to state the problem: S% of the portfolio is invested in stocks; stock prices drop by x%. I was afraid if I said S of the portfolio is invested in stocks and stock prices drop by x, it’s not very clear what S and x mean. The charts are more interesting than the formulas.
Did you do the exercise with the extra variable b? Or take it one step further and make the band threshold t as opposed to a constant 5%?
ajk says
I just like decimals when doing math with percents. You used whole numbers three different places, which is why you needed to adjust to 0.05 by a factor of 100 ^3 = 1 million to 50,000.
Also, note that, while your problem is not exactly the same, it is similar to if your stock drops by 25%, it has to come up by 33.33% to get back. For example, after a drop of 19% from 1 to 0.81, you need a gain of 1/.81 -1 = .235 (23.5%) to get back to even. This is close to the numbers you have for going from 60% to 55% (19%) and from 60% to 65% (24%). The difference is that (I think) I am going from 60% to 55% and then from 55% to 60%. Slightly different problem, but close enough to have similar answers.
And no, I didn’t do anything other than use decimals in your first two formulas.
nickel says
So… I just looked more closely at the graph, and it’s quite interesting that, even in the mid-range, you need close to a 20% change in the stock market to trigger a rebalance. I never realized it had to be such a major swing. Of course, you’re holding bonds constant. If they’re changing in the opposite direction, then it’s a somewhat different story.
Harry Sit says
@JimInIllinois – I forgot how to do calculus already. Can you explain why “The sensitivity of the stock or bond percentage to changes in stock prices minus changes in bond prices is the fraction in stocks times the fraction in bonds”?
@ajk – I agree using decimals will make the formula easy to remember. The generic formula is:
x = t * (1 + b) / S / (1 – t – S) + b
where
t = rebalancing threshold, up 5% = +0.05, down 5% = -0.05
b = bond price change, up 1% = +0.01, down 1% = -0.01
S = starting weight of stocks, 60% = 0.6
@nickel – I was surprised by the required 20% swing as well. Apparently @JimInIllinois figured this out a long time ago.
If you use the above generic formula, you will see you basically add or subtract the bond price change to the required stock price change. At t = -0.05, b = +0.02, S = 0.6,
x = -0.05 * 1.02 / 0.6 / 0.45 + 0.02 = -0.17
which means stocks will have to go down 17% to move the stock percentage from 60% to 55% if bonds go up by 2% at the same time.
Finally, the Japan problem can’t be solved by delaying rebalancing or not rebalancing at all. It has to be solved by diversification and by not participating in bubbles. The EAFE index, although dominated by Japan in early 1990s, did OK. Many actively managed funds underweighted Japan during that time.
JimInIllinois says
@TFB – here’s the math:
Let S be the initial fraction of your portfolio in stocks, so 1-S is the initial fraction in bonds. If the value of stocks change by F% then the value of your portfolio increases by S*F%, the fraction in stocks times the fractional increase in stock value. Your new stock ratio is (S+S*F)/(1+S*F). The derivative (slope) of this with respect to F is (S*(1+S*F)-S*(S+S*F))/(1+S*F)^2, which at F=0 is S*(1-S). Recall that 1-S is your initial fraction in bonds. So, if stocks go up F%, your portfolio value goes up S*F% but the fraction of your portfolio in stocks only goes up S*(1-S)*F%. On the other side, if bonds go up G%, your portfolio value goes up (1-S)*G%, and the fraction of your portfolio in stocks goes *down* S*(1-S)*G%. Since your asset allocation adds to 100%, the bond fraction change is the negative of the stock fraction change. Since we are assuming small changes in this first-order approximation you can add them together to get a total stock fraction change of S*(1-S)*(F%-G%).
nickel says
I agree that not rebalancing doesn’t solve the Japan problem, but it was interesting to me to see the numbers showing that rebalancing actually made things worse because in that case.
anon says
Your definition of “5% band” is odd.
If my AA is say 60:40 then five percent of sixty is three percent.
So when stocks equal either 57% or 63% I will rebalance.
Sai says
This presentation is amazing, an eye opener for me. Thank you.
Marlowe says
June 2016: I am currently re-evaluating my exposure to equity as I see valuations and profit margins at unsustainable levels. This is a very helpful tool as I build a strategy for the uncertainty of next 24 months. Rather than speculating and “jumping out” of equities, this gives me reasonable expectation of my potential for loss and how it will impact my portfolio.
Andy says
6Why would you want a band that is a fixed percentage of the total, rather than a percentage of the allocation? For example, if I like having a 5% REIT allocation, and it had a huge drop, why would I wait until it dropped 5% (to 0%) before re-investing?
What makes more sense to me (and is advocated by William Bernstein in his Investing for Adults series), are bands that are a percentage of the allocation.
So, let’s say the band is 20% of the allocation. Thus, for your 5% REIT, you’d rebalance when REITS are 20% up (when REITS hit 6% of your portfolio) or 20% down (4%). In other words, when REITS are 120% or 80% of the amount you want in REITS. For a much larger stock allocation of 50%, you’d balance at 20% up (60% of your overall portfolio) or 20% down (when it hits 40% of your total allocation).
Intuitively, this makes sense. If asset X goes up 20% or down 20% in value, it is probably time to bring it back in line with what you originally intended. 20% is a pretty large movement, so it should lead to pretty infrequent rebalances, which is desirable from a fee-efficiency perspective.
Actually, Bernstein recommends (and I have in my tracking spreadsheet) log-based bands, so the upside end of the band is larger than the downside. You’re actually talking about ratios. So, for a 20% upside band, you’d rebalance at either 6/5 of target, or 5/6 of target, meaning your bands are between 83% and 120% of your allocation in that particular asset class.
Harry Sit says
The 5% threshold is applied to the broad asset classes: stocks vs bonds. It’s not applied to a sub asset class within stocks.
Andy says
That makes more sense, but isn’t stated explicitly in the article. Because obviously as your chart shows, this rule tends towards the ridiculous as you reach the edges. If a person thinks a 10% stock allocation is proper, she really doesn’t want to wait for a 53% drop in the stock market before she buys more stocks. She will miss a lot of opportunities to buy low if she does.
Harry Sit says
The second paragraph. The entire post talks about stocks vs bonds. It only says the 5% band is a popular method, not whether any specific investor should adopt it or not. Whether you are at the edge or in the middle, the maximum you will miss in buying stocks on the cheap is the same: 5% of your portfolio size.
Grant says
Actually, Larry Swedroe suggests the bands be an absolute 5% or a relative 25%, which ever comes first. This is essentially what Bill Bernstein is advocating combined with the 5% rules
Harry Sit says
When applied at the highest level, stocks vs bonds, as discussed here, absolute 5% always comes first when your target allocation is between 20% stocks and 80% stocks.
Jim says
Interesting how large the percentage is to hit a 5% band. I always suggest people translate that into dollars. When you have a large portfolio sometimes the percentages seem a bit scary but when you translate that into dollars it can be a nightmare. I find that many entering retirement tend to go on cruise control as far as their allocations not necessarily realizing the dollars at risk that might be much harder to replace as human capital plunges.
Brad says
+1 !!!
Brad says
I think your insight that “Because the market goes up more often than down, perhaps asymmetric bands are in order, say 7% up, 3% down?” is quite useful. I would imagine that Vanguard researchers, Wealthfront, Betterment, etc. and all the asset allocating indexers out there have likely already figured out the optimal asymmetry needed for rebalancing in a generally upward market which returns over long-term averages about (positive) +9% a year or so; this asymmetry should be adjusted for each asset type based on their very long-term positive average uptrend, I’d assume.
Kyle says
Interesting analysis. For those interested, I think Kitces (https://www.kitces.com/blog/best-opportunistic-rebalancing-frequency-time-horizons-vs-tolerance-band-thresholds/) completed a really interesting approach on rebalancing. I have enabled it in my portfolio and find it accretive.