Lump Sum, Dollar Cost Average, Or Wait for Dip?

It’s December. A new year is just around the corner. I’m thinking of when I should contribute to my IRA for the next year.

In the past, I always contributed the full amount at the first opportunity: January 2. Every year I just moved $5,000 or whatever the limit was for that year from my savings account to my IRA on January 2. The savings account would build back up later.

Generically speaking, this is lump-sum investing. Theory says because the market tends to go up over time, you should give the money maximum time exposure in the market: the earlier the merrier.

The reality of course isn’t as neat as the theory. The value of the fund shares that I bought in January each year invariably went down during the year, sometimes by a lot. If I had waited, I could’ve bought more shares at a lower price with my annual contribution. For next year, should I (a) go all in on January 2; (b) spread it throughout the year; or (c) wait for a lower price and then jump in?

I read somewhere from someone that the low point of the market during a year is almost always on a day other than January 2. On the surface this is too obvious. Of course the low in the year wouldn’t always occur on January 2. There are 250 trading days in a year. It’s highly likely that the low of the year would happen after January 2.

Although nobody knows exactly when the price will be the lowest in a year, that’s not the point. If you can be reasonably confident that the low point is going to be at least X% lower than the price on January 2, you can just set a trigger to buy when the price goes X% lower. It’s OK if it’s not the lowest point. You are not trying to catch the lowest. You just want to beat the price on January 2.

Beating the price on January 2 will also beat the market for that year because the market performance is measured from the beginning of the year. Is it this simple to beat the market? Enter a limit order at X% below the price on January 2, sit back and wait? At what level should the trigger be set to avoid the problem of waiting forever?

I did a quick study. I downloaded the calendar year open and low prices for S&P 500 from 1950 to 2011. I chose S&P 500 only because it’s easy to get data. There are 62 data points. Here’s the chart:

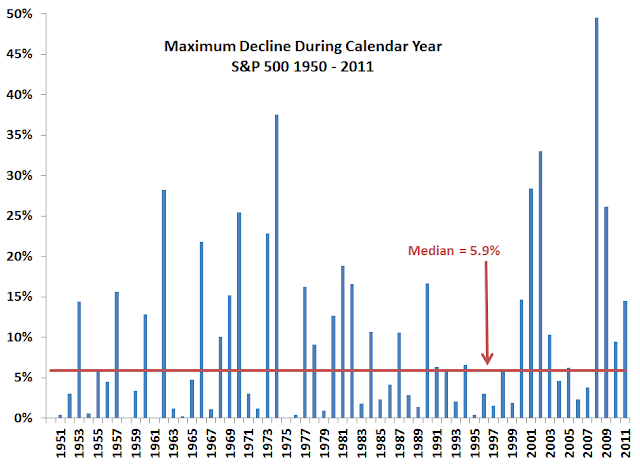
Here’s a summary:

	Price Drop During Calendar Year
Minimum	0%
Maximum	50%
Mean	9.6%
Median	5.9%

In 4 out of 62 years, the price on January 2 was actually the lowest in the year. In the worst year (2008), the price went down by 50% from what it was on January 2. The average decline during a calendar year was 9.6%. The median was 5.9%, which means that in 31 out of 62 years the price dropped more than 5.9% during the year, and in the other 31 years it dropped less.

Obviously setting the trigger at 5.9% won’t work very well. 50% of the time you’d be sitting there all year and not catching a lower price. The bar has to be set lower. How much lower though?

I grouped the calendar year drops by percentile.

Down By This Much During the Year	% of Observations
> 1%	84%
> 2%	73%
> 3%	61%
> 5%	52%
> 10%	39%
> 15%	24%
> 20%	15%

The data are crowded at both ends. 16% of the time the market saw a drop less than 1% during the year, yet 39% of the time it saw a drop greater than 10%.

If I don’t get greedy and I set the trigger point at 2%, I’d be successful roughly 3 out of 4 times. That’s not bad. I heard studies that say lump-sum investing beats dollar cost averaging 2 out of 3 times. If that’s good enough to favor lump-sum investing, beating it 3 out of 4 times with a 2% price drop trigger would be even better.

The downside of this kind of strategy would be that you pick up 2% in 3 out of 4 years and then you give back 10% in the fourth year when the price just goes up and up. The same can be said about lump-sum versus dollar cost averaging though. Going all in on January 2 may beat monthly dollar cost averaging in 2 out of 3 years but when you get a year like 2008, dollar cost averaging would make it all back.

I may just try the 2% trigger in 2012 and see what happens. How will you make your contributions, lump sum in January, spread it out, or wait for a good price?